BQ # 7: Unit V: The Difference Quotient and The Derivative

1). Where the difference quotient actually comes from

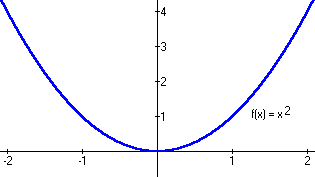
If we take a normal graph, such as the one above, we can easily derive the difference quotient formula. We make a point with an x value of  'x' and the distance from that point to the origin is therefore 'x'. The y-coordinate of the point would be f(x), which just means whatever y would be when 'x' is plugged into the equation of the graph. If a distance of 'h' is added to the distance of 'x', we get an overall distance of x + h where another point with an x- value of 'x+h' is located. The y-value of that second point would be f(x+h).

Next, all we do is apply the slope formula, which is (ysub2 - ysub1 / xsub2 - xsub1). As shown in red in the picture, when we apply this formula to our two points on the graph, we get the difference quotient formula after simplification.

2). How this is relevant to our lessons of derivatives

Since the difference quotient  basically represents the slope of a line that touches two points on a graph (shown above), and a secant line is a line that meets a graph in two points at given slopes, the difference quotient could be used to find the slope of secant lines wherever those two points may be. In other words, in Calculus the difference quotient represents the slope of secant lines.

BUT WAIT! THERE'S MOREEE

The difference quotient may give us the slope of secant lines, however, they fail to give us the slope of lines that touch ONLY 1 POINT, which are known as tangent lines. In order to do this, we must find what is known as the derivative, which is the equation that represents the slope of tangent lines. In order to get this we must evaluate the limit as h approaches zero of the equation we got from the difference quotient. We do this because 'h' (as noted above) is the distance between the two points on the graph. In a secant line there is two points, and in a tangent there is only one, so how do we get the derivative from a secant line? The answer is clear: we make h, the distance between the two points as close to 0 as possible, because when h is zero, there is only one point, but h can never actually reach zero in a secant line so thus we evaluate the limit as h approaches zero in order to get the derivative which represents the tangent line.

A tangent line of a function with a point at (0, 0)

A secant line of the same function where h = .2

A secant line of the same function where h = 2.5

As displayed above, the closer h is to zero, the closer the secant line resembles the tangent line. This is the reason why we evaluate the limit as h approaches zero of the equation from the difference quotient, which represents the secant line approaching zero, or becoming the tangent line.

Sources

Last three pictures: desmos.com

BQ #6: Unit U: Continuity and Limits

1). What is continuity? What is discontinuity?

• Continuity in Calculus basically means that a graph is continuous which means that the graph has 4 characteristics: 1). the graph can be predicted, 2). the graph contains no breaks, no holes, no jumps, and no oscillating behavior, 3). the value and the limit must be the same, and 4). the graph must be able to be drawn without the lifting of the pencil from the paper.

An example of a continuous graph with all 4 characteristics of continuity
http://www.hyper-ad.com/tutoring/math/calculus/Derivatives.html

• Discontinuity in Calculus is, consequently, something that that causes a graph to be discontinuous. There are 4 types of discontinuities, which are divided into 2 families, these being Removable and Non-Removable.Removable discontinuities include point discontinuities, which are essentially just holes. Non-Removable include jump discontinuities, which cause breaks in the graph, infinite discontinuities, which result in unbounding behavior, and oscillating behavior, which creates unpredictable, random "wiggly lines". 

A point discontinuity, creating a hole
http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity

A jump discontinuity resulting in a break in the graph
http://en.wikipedia.org/wiki/Classification_of_discontinuities

A vertical asymptote causes an infinite discontinuity
http://www.emathematics.net/continuity.php?def=discont

Oscillating behavior causing discontinuity
http://web.cs.du.edu/~rjudd/calculus/calc1/notes/discontinuities/

2). What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

• A Limit is the intended height of a function.A limit EXISTS when the specific interval of the graph where the limit is located is CONTINUOUS. In other words, if a limit is located at a part of the graph that has all 4 characteristics of a continuous function, then the limit will exist. The reason behind this is that only when a graph is continuous does the graph have a consistent intended height; when a graph is discontinuous it has certain abnormalities that cause the intended height to be inconsistent and undefinable.
• A limit, however, does not exist when the intended height of a function is unclear or inconsistent due to the presence of any of the three Non-Removable discontinuities.There are 3 specific cases of this happening. In the first case, the graph as it approaches the limit shows different left and right behavior, meaning that as the graph is getting to the limit from the left and from the right two different locations are reached and thus two different intended heights are apparent and thus a single limit does not exist. This is because of a jump discontinuity.In case 2, the graph may exhibit unbounded behavior due to an infinite discontinuity due to a vertical asymptote. This results in the graph to go in unbounded directions, and as a result the limit will never exist where the asymptote is because a limit can never intend to reach a height of infinity. Thirdly, if there is oscillating behavior, the graph is so unpredictable that a graph has no real intended height.
• It is important to discern between a value and a limit. A value is the actual height of a function whereas a limit is the intended height. Sometimes these are both the same thing, but a lot of other times they are not. For instance, in the case of a hole, the limit is at the hole, but there is no value at a hole. On the other hand, there can be a value but no limit, such as the case in the jump discontinuity below:

The value is at the closed circle, however at that same value of x, there is no limit because of different left and right behavior due to the jump.
http://commons.wikimedia.org/wiki/File:Jump_discontinuity_cadlag.svg

3). How do we evaluate limits numerically, algebraically, and graphically?

• A limit can be evaluated numerically through the means of a table very similar to a number line. What we do is we use what x is approaching and list out  x- values that are mere tenths, hundredths, and thousandths away from that number and then find the y values to see what the limit is. For instance, if we wanted to evaluate a limit of a function as x approaches 4, we would make a x-y table and put 4 in the middle of the x section and then on the far left put 3.9 and on the far right 4.1, then we simply get closer to 4 with the x values and we plug the equation into a graphing calculator and trace the values for our x's. We can then observe what the limit is.
• A limit can be evaluated graphically evaluated very easily. Simply get a graph and move your fingers from the left and right of the where the limit should be. If they meet, then the limit exists. If not, the limit does not exist.
• Evaluating algebraically can involve three different methods. These are direct substitution, factoring/dividing method, and the rationalizing/conjugate method. 
• In direct substitution we just plug in what x is approaching into all the places an 'x' is in the function. We can get four answers from this: a number value, zero, undefined (meaning there is a vertical asymptote/infinite discontinuity or a hole), or indeterminate form (0 divided by 0) which means we got to use an additional method.
• In the factoring/dividing out method we factor both denominator and numerator in order to see if a hole cancels out so we can use direct substitution with the result to get the limit.
• In the rationalizing/conjugate method, we have to multiply by a conjugate to try to get something to cancel (something that we can't factor in the first place) and then we resume with direct substitution.

Sources:

http://www.hyper-ad.com/tutoring/math/calculus/Derivatives.html - the first image

http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity - second image
http://en.wikipedia.org/wiki/Classification_of_discontinuities - 3rd
http://www.emathematics.net/continuity.php?def=discont - 4th
http://web.cs.du.edu/~rjudd/calculus/calc1/notes/discontinuities/ - 5th
http://commons.wikimedia.org/wiki/File:Jump_discontinuity_cadlag.svg - 6th

BQ #4: Unit T Concepts 3: Tangent and Cotangent Graphs

1). Why is a "normal" tangent graph uphill but a "normal" cotangent graph is downhill?

The reason for this is that tangent and cotangent have different ratios that cause for the asymptotes to be in different places.

http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Bruce/instructunit/day_6.htm

•  The ratio for tangent in terms of sine and cosine is sine/cosine. As a result, tangent will have asymptotes whenever and wherever cosine is on the x- axis (when cosine is equal to zero).
• In order for tangent to follow its ASTC pattern  (positive, negative, positive, negative), the uphill shape shown above occurs in accordance with its asymptotes.

https://share.ehs.uen.org/node/19145

 

 

•  Cotangent, on the other hand has asymptotes wherever sine is equal to zero on the y-axis because the trig ratio is cosine/sine.
• The difference in the asymptote location causes for the differences in shape. Since cotangent and tangent follow the same ASTC pattern, they both are positive is quadrants I and III and negative in II and IV. In order for cotangent to follow this pattern, it must be downhill.

Used Websites: http://jwilson.coe.uga.edu/EMT668/EMAT6680.2001/Bruce/instructunit/day_6.htm
(tangent picture)
https://share.ehs.uen.org/node/19145 (cotangent picture)

BQ #5: Unit T Concepts 1-3: Trig Graphs and Asymptotes

1). Why are sine and cosine the only trig graphs that have asymptotes?

• As we can see from the above picture, sine and cosine have unique ratios when compared with all the other trig values. They both have a denominator of r. In the Unit Circle, r is always equal to 1. Now, the question is why don't sine and cosine have asymptotes whereas all the other ratios do?
• We get an asymptote whenever we divide by zero (in other words, whenever we have a denominator of zero.) This results in undefined answers, in which an asymptote accounts for.
• Sine and cosine have denominators of r which is always equal to one in this case. Therefore when using sine and cosine we will never be dividing by zero and never be getting asymptotes.
• The rest of the trig functions, however, have denominators of x and y. These denominators can be any number, and when that number is zero, then you will get undefined and therefore an asymptote.

BQ #3: Concepts 1-3: Graphing Trig Graphs

1). How do the graphs of sine and cosine relate to the others? (With an emphasis on asymptotes)

Well then, the very first thing you need to answer this is, what do ya know, the graphs. Who would've thought that, right? Anyhow, here goes nothing...

a). Tangent in relation to sine and cosine

• Here we see a graph of sine, cosine, and tangent (black) as well as some asymptotes (various shaded regions). Focus on the light green and orange regions. It is in these two regions that tangent is a full period, therefore we can observe the relationship it has according to its asymptotes through these regions. We can see that asymptotes occur wherever cosine (green) has a point on the x-axis (in other words a value of zero.)  This corresponding relationship can be explained in the trig ratio: tan = sin/cos. Since we know that we get asymptotes by dividing by zero, using this trig ratio we know that there will be an asymptote whenever cosine, the denominator, is zero.

b). Cotangent in relation to sine and cosine

• Here is the same graph with cotangent instead of tangent. We can apply the same logic to this one as we did above. Since cot = cos/sin, there will be an asymptote wherever the sine value is zero.

c). Secant in relation to cosine

• Shown here is cosine (middle and green) and secant (top/bottom and blue). Since secant is the reciprocal of cosine, it's relationship to the cosine graph is affected in various ways. The most obvious is the x-axis reflection of the peaks and valleys of the cosine graph. However, what we are looking for is how this relationship causes the asymptotes (black dotted lines). The reason asymptotes are there is once again because of a trig ratio, this time being that sec = 1/cos, and like before, since cosine is the denominator, any place where the cosine value is zero we will have an asymptote.

d). Cosecant in relation to sine

• This one is just like the secant and cosine graphs. The only difference is that the ratio applied is csc  = 1/sin and therefore wherever the sine value is equal to zero on the x- axis then there will be an asymptote.

BQ #2: Unit T Concept 1 Intro: Trig Graphs and the Unit Circle

1). How do Trig Graphs relate to the Unit Circle?

Trig graphs relate to the unit circle in that they follow the same pattern that is defined by ASTC in the Unit Circle in their periods, which is the length of each cycle in the graphs. As a result of this, the trig graphs are basically just "unraveled" versions of the unit circle.

Why do sine and cosine have periods of 2 pi and tangent and cosine have periods of just pi?

• This is can be explained through the Unit Circle and ASTC patterns that are repeated through the periods, as mentioned above. In order to fully understand this, the picture below shows this relationship.

• On the top is ASTC and the Unit Circle, and on the bottom are the trig graphs. Note how for sine and cosine it takes a full revolution of the unit circle in order to repeat the pattern of the signs. A full revolution is 2 pi. Since trig graphs follow the same pattern, it would take 2pi to repeat the +/- pattern and thus the period would be 2pi. However, take note of the tangent and cotangent pattern. This pattern only requires 1/2 a revolution, or just pi, to repeat itself and thus the period is just 1 pi for tangent and cotangent.

Why are Sine and Cosine graphs the only ones with amplitudes (in reference to the unit circle)?

• When we look at the different types of graphs, we notice that sine and cosine have infinite domain but restricted range. This calls need for amplitudes, which define the range of such graphs.
• But why does this occur? If we refer back to the trig ratios of the Unit Circle, we know that sine and cosine are the only two with denominators of r, which is always 1 on the Unit Circle. As a result, Sine and Cosine could be no bigger than 1, otherwise the ratio would cause for a point not on the unit circle resulting in no solution.  Thus, amplitudes are needed in trig graphs in order to ensure that the graph stays in this zone.

Click to see website

This illustrates the above mentioned information of the Unit Circle's limitations on sine and cosine. Amplitudes are needed to make sure the graph stays within such restriction.

Citations: http://htmartin.myweb.uga.edu/6190/functions3.html Unit Circle Trigonometry

Reflection #1: Unit Q: Verifying Trig Identities

1). To verify an identity means to prove that it is true. For example, an identity might be one equation or term that is equal to another and you have to prove that to be true using your knowledge of identities and your knowledge of simplification processes.

2). I have found that in verifying identities there are always the same strategies being repeated. These strategies include finding a GCF or a LCD, multiplying by the conjugate, separating fractions, converting into sine and cosine, using the zero product property, etc. Of these, I have found that converting into sine and cosine and separating fractions (only those with a monomial denominator) are two of the most recurrent and helpful strategies at approaching a problem. I also like to look at the answer when verifying to see if I can find any hints as to what to do to get there. Lastly, I also always look for things that might cancel each other out, since they can be very helpful.

3). I always ask myself when doing these problems "what can I do to change the problem in order to be able to use identities to get the answer?". Usually I look for anything that might hint toward a specific identity. For example, if I see cosine squared  and sine squared I know I am going to be using a Pythagorean identity. Sometimes the problem is more complicated and you might have to alter it a bit before any identity jumps out in front of your face. A common example of this would be if you have to factor the problem first in order to get something that you can use.

SP #7: Unit Q Concept 2: Finding all trig functions using idenitites

This blog post was made through the infallible alliance that is between the juggernaut forces of Omar "Ice" T. and Michael "Vitamin" C. Any illegal publishing of this copyrighted post without the consent of the above mentioned is strictly prohibited and is punishable by permanent imprisonment or death (whichever comes first). To see various other posts by Omar "Ice" T., feel free to click here.

 This is our problem. We are given that cotangent is 7/8 and sine is negative. Also we know that the problem lies in the third quadrant since tangent is positive and cosine is negative according to ASTC. We use what we know about identities to solve for the rest of the trig functions. We will then check our answers by solving with the unit circle, which we learned in Unit N or by using SOH CAH TOA from Unit O.

 One of the easiest things to do is find tangent which is the inverse of cotangent. Knowing this, when we use the reciprocal identities we find that tangent is equal to 8/7.

 Now that we know tangent we can use a Pythagorean identity to find secant. Secant ends up being equal to radical113 divided by 7.

 Cosine is the inverse of secant, which we just found, so we are able to use a reciprocal identity using secant to find cosine. Cosine will be 7 rad 113/ 113.

 First here we find sine using a Pythagorean identity and we can do this since we have found the value of cosine. We then find cosecant by doing the inverse of sine, also known as using a reciprocal identity.

 We have now found all the trig functions using identities. Note that all the answers except tangent and cotangent are negative because the problem lies in quadrant III.

Here is the same problem done using SOH CAH TOA. Note that the answers are identical with the answers found using identities.

1).  It is important to know several things in doing this problem. One must pay attention to what identity is being used to solve for each function. There are different ways to find each function with different identities but one must make sure that there is only one unknown trig function when plugging into an identity. Also, one must make sure to get their signs correct by understanding how we found what quadrant the answer was in and what effect that quadrant has on the answers.

I/D #3: Unit Q Concept 1: Pythagorean Identities

Inquiry Activity Summary:

 1). An identity is a proven fact or formula that is always true. Pythagorean Identities are proven to be true and are one type of identities that we are studying in this concept. They can be easily derived through our knowledge of the Pythagorean theorem and the Unit Circle. The following will show precisely how I have done just that.



 

 

 

• So basically what I did was I wrote out the Pythagorean theorem and then made it equal to 1 by dividing everything evenly by r squared. I then used what I knew of the trig functions, specifically the ratios of sine and cosine to rewrite the equation. The end result was the first Pythagorean identity.
• The next thing I did was I tested the truth of the equation. I used what I knew of the Unit Circle to get a point (in this case the point for 45 degrees) and plugged in the cosine and sine values of that point into the equation. The equation met expectations, meaning that the equation is indeed an identity.

 

2). The other two main identities of the Pythagorean Identities can be derived by



simply by dividing by either cosine squared or sine squared from the first identity.

• After dividing by cosine, the cosines will cancel into a 1 and using the ratio and reciprocal identities we find that we are left with tangent and secant. The result is the second Pythagorean identity.
• After dividing by sine we find that like the other one, something cancels into a one and the trig functions change (this time into cotangent and cosecant). The result this time is the third main Pythagorean identity.

Inquiry Activity Reflection:

1). The connections I see between Units N, O, P, and Q so far are that the identities are related to the Unit Circle (Unit N) in that we use an r value of 1 for the Pythagorean theorem and we use the sine and cosine of a point on the unit circle to test the equation and that we use the relationships of the various trig functions to do the derivations. We also use the Pythagorean in the other derivations we have done for the various other units.

 

2). If I had to describe trigonometry in three words they would be: integrated, complex, and understandable.

 

 





WPP #13-14: Unit P Concepts 6-7: Law of Sines and Law of Cosines

This blockbuster of a blog post was a co-op with the ingenuous swag of Omar T. To view the actual blog post along with some more swaggy content, please do not hesitate to click here.

BQ #1: Unit P Concepts 1-3 and 4-5: Law of Sines (Derivation) and Area Formulas (Oblique Derivation)

1). Deriving the Law Of Sines:

The Law of Sines is used to solve non-right triangles, specifically ones in which we already know or are given two angles and a side either after the two angles or between the two angles (non-right triangles with AAS or ASA relationships). This is useful because most triangles are not right triangles.  The Law of Sines is as depicted below:


http://www.mathwarehouse.com/trigonometry/law-of-sines/formula-and-practice-problems.php

We can derive the Law of Sines with a normal oblique triangle. The following are the steps by which this is done:

http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm

• We first draw a non-right triangle and label the sides and angles respectively.  We then draw a height (h) perpendicular down from angle B, making two right triangles.

• Now, using basic trig functions, we could see that sinA = h/c and sinC = h/a. If we solve for "h" in both equations we get csinA = h and asinC = h. Since both csinA and asinC are now equal to h, they are also both equal to each other (Transitive Property).

• Set csinA and asinC equal to each other. Divide by ac on both sides and we get the Law of Sines (sinA/a = sinC/c). Say we used  angle B instead of angle C, we should get sinA/a = sinB/b , and since they are all equal to each other, the order can be switched around to make the whole Law of Sines: sinA/a = sinB/b = sinC/c.

4). Area Formulas: Deriving the Area of an Oblique Triangle formula

The formula for the area of a triangle is A = 1/2bh and this works fine with right triangles since h is just one of the sides. But with an oblique triangle, h, which is the height of the triangle, is a little more complicated. Thus there is a distinct way to find the area of an oblique triangle, in which the value of h is unknown. The following steps walks through how we come up with this distinction in the area formula:

•  First draw your oblique triangle and label the sides and angles. Draw the height of the triangle (h). We know that the area of the triangle is 1/2 times the product of the base and the height, but what's h?

• Similar to what we did for the law of sines, if we take the sine of angle C we see that sinC = h/a. We can then solve for h and we get h = asinC. We now have a value for h, which we can plug back into the area formula.

• We have taken our value for h and plugged it back into the area formula. All you need to fund the area using this formula is two sides and the sine of the angle between them (SAS), in this case our two sides would be side b and side a, and angle C would be between them. We can see that this is essentially the same formula as the original area formula for a triangle; the only difference is we have to find and use a certain substitute value for h because the height is not always given in an oblique triangle.

References:

First Picture: The Law of Sines: http://www.mathwarehouse.com/trigonometry/law-of-sines/formula-and-practice-problems.php

Second Picture: Deriving Law of Sines: http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm