1). Deriving the Law Of Sines:
The Law of Sines is used to solve non-right triangles, specifically ones in which we already know or are given two angles and a side either after the two angles or between the two angles (non-right triangles with AAS or ASA relationships). This is useful because most triangles are not right triangles. The Law of Sines is as depicted below:
| http://www.mathwarehouse.com/trigonometry/law-of-sines/formula-and-practice-problems.php |
 |
| http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm |
- We first draw a non-right triangle and label the sides and angles respectively. We then draw a height (h) perpendicular down from angle B, making two right triangles.
- Now, using basic trig functions, we could see that sinA = h/c and sinC = h/a. If we solve for "h" in both equations we get csinA = h and asinC = h. Since both csinA and asinC are now equal to h, they are also both equal to each other (Transitive Property).
- Set csinA and asinC equal to each other. Divide by ac on both sides and we get the Law of Sines (sinA/a = sinC/c). Say we used angle B instead of angle C, we should get sinA/a = sinB/b , and since they are all equal to each other, the order can be switched around to make the whole Law of Sines: sinA/a = sinB/b = sinC/c.
4). Area Formulas: Deriving the Area of an Oblique Triangle formula
The formula for the area of a triangle is A = 1/2bh and this works fine with right triangles since h is just one of the sides. But with an oblique triangle, h, which is the height of the triangle, is a little more complicated. Thus there is a distinct way to find the area of an oblique triangle, in which the value of h is unknown. The following steps walks through how we come up with this distinction in the area formula:- First draw your oblique triangle and label the sides and angles. Draw the height of the triangle (h). We know that the area of the triangle is 1/2 times the product of the base and the height, but what's h?
- Similar to what we did for the law of sines, if we take the sine of angle C we see that sinC = h/a. We can then solve for h and we get h = asinC. We now have a value for h, which we can plug back into the area formula.
- We have taken our value for h and plugged it back into the area formula. All you need to fund the area using this formula is two sides and the sine of the angle between them (SAS), in this case our two sides would be side b and side a, and angle C would be between them. We can see that this is essentially the same formula as the original area formula for a triangle; the only difference is we have to find and use a certain substitute value for h because the height is not always given in an oblique triangle.
References:
First Picture: The Law of Sines: http://www.mathwarehouse.com/trigonometry/law-of-sines/formula-and-practice-problems.phpSecond Picture: Deriving Law of Sines: http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm




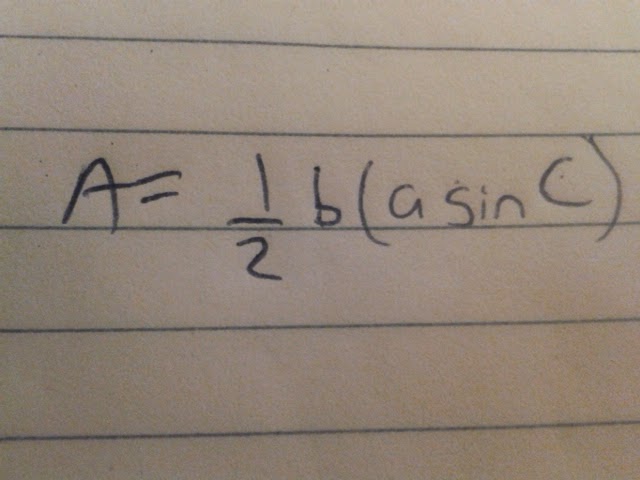
No comments:
Post a Comment