Dem Mathematical Feelz: BQ #6: Unit U: Continuity and Limits

1). What is continuity? What is discontinuity?

Continuity in Calculus basically means that a graph is continuous which means that the graph has 4 characteristics: 1). the graph can be predicted, 2). the graph contains no breaks, no holes, no jumps, and no oscillating behavior, 3). the value and the limit must be the same, and 4). the graph must be able to be drawn without the lifting of the pencil from the paper.

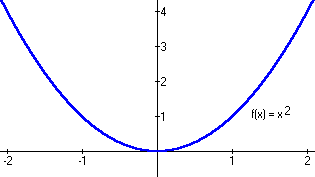An example of a continuous graph with all 4 characteristics of continuity
http://www.hyper-ad.com/tutoring/math/calculus/Derivatives.html

Discontinuity in Calculus is, consequently, something that that causes a graph to be discontinuous. There are 4 types of discontinuities, which are divided into 2 families, these being Removable and Non-Removable.Removable discontinuities include point discontinuities, which are essentially just holes. Non-Removable include jump discontinuities, which cause breaks in the graph, infinite discontinuities, which result in unbounding behavior, and oscillating behavior, which creates unpredictable, random "wiggly lines".

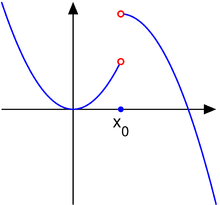
A point discontinuity, creating a hole
http://www.wyzant.com/resources/lessons/math/calculus/limits/continuity

A jump discontinuity resulting in a break in the graph
http://en.wikipedia.org/wiki/Classification_of_discontinuities

A vertical asymptote causes an infinite discontinuity
http://www.emathematics.net/continuity.php?def=discont

Oscillating behavior causing discontinuity
http://web.cs.du.edu/~rjudd/calculus/calc1/notes/discontinuities/

2). What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A Limit is the intended height of a function.A limit EXISTS when the specific interval of the graph where the limit is located is CONTINUOUS. In other words, if a limit is located at a part of the graph that has all 4 characteristics of a continuous function, then the limit will exist. The reason behind this is that only when a graph is continuous does the graph have a consistent intended height; when a graph is discontinuous it has certain abnormalities that cause the intended height to be inconsistent and undefinable.
A limit, however, does not exist when the intended height of a function is unclear or inconsistent due to the presence of any of the three Non-Removable discontinuities.There are 3 specific cases of this happening. In the first case, the graph as it approaches the limit shows different left and right behavior, meaning that as the graph is getting to the limit from the left and from the right two different locations are reached and thus two different intended heights are apparent and thus a single limit does not exist. This is because of a jump discontinuity.In case 2, the graph may exhibit unbounded behavior due to an infinite discontinuity due to a vertical asymptote. This results in the graph to go in unbounded directions, and as a result the limit will never exist where the asymptote is because a limit can never intend to reach a height of infinity. Thirdly, if there is oscillating behavior, the graph is so unpredictable that a graph has no real intended height.
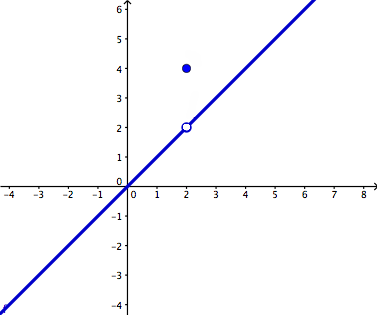
It is important to discern between a value and a limit. A value is the actual height of a function whereas a limit is the intended height. Sometimes these are both the same thing, but a lot of other times they are not. For instance, in the case of a hole, the limit is at the hole, but there is no value at a hole. On the other hand, there can be a value but no limit, such as the case in the jump discontinuity below:

The value is at the closed circle, however at that same value of x, there is no limit because of different left and right behavior due to the jump.
http://commons.wikimedia.org/wiki/File:Jump_discontinuity_cadlag.svg

3). How do we evaluate limits numerically, algebraically, and graphically?

A limit can be evaluated numerically through the means of a table very similar to a number line. What we do is we use what x is approaching and list out x- values that are mere tenths, hundredths, and thousandths away from that number and then find the y values to see what the limit is. For instance, if we wanted to evaluate a limit of a function as x approaches 4, we would make a x-y table and put 4 in the middle of the x section and then on the far left put 3.9 and on the far right 4.1, then we simply get closer to 4 with the x values and we plug the equation into a graphing calculator and trace the values for our x's. We can then observe what the limit is.
A limit can be evaluated graphically evaluated very easily. Simply get a graph and move your fingers from the left and right of the where the limit should be. If they meet, then the limit exists. If not, the limit does not exist.
Evaluating algebraically can involve three different methods. These are direct substitution, factoring/dividing method, and the rationalizing/conjugate method.
In direct substitution we just plug in what x is approaching into all the places an 'x' is in the function. We can get four answers from this: a number value, zero, undefined (meaning there is a vertical asymptote/infinite discontinuity or a hole), or indeterminate form (0 divided by 0) which means we got to use an additional method.
In the factoring/dividing out method we factor both denominator and numerator in order to see if a hole cancels out so we can use direct substitution with the result to get the limit.
In the rationalizing/conjugate method, we have to multiply by a conjugate to try to get something to cancel (something that we can't factor in the first place) and then we resume with direct substitution.